Fotony - kwanty promieniowania elektromagnetycznego - oddziaływają z materią na wiele sposobów. Trzy z nich odgrywają zasadniczą rolę: zjawisko fotoelektryczne, efekt Comptona i produkcja par elektron-pozyton. Dwa pierwsze z nich już rozpatrywaliśmy omawiając, kwantowe cechy promieniowania elektromagnetycznego, trzeci proces omówimy poniżej.
Teraz skupimy uwagę na tych cechach oddziaływania fotonów z materią, które dotyczą przekazu energii i absorpcji promieniowania. Każdy z procesów reprezentowany jest symbolicznym rysunkiem. (Pamiętajmy jednak, że rysunki te nie odzwierciedlają bynajmniej relacji geometrycznych czy kinematycznych, ale maja za zadanie zilustrować poglądowo mechanizm zachodzenia poszczególnych procesów.) Prawdopodobieństwa ich zachodzenia zależne są od energii fotonów oraz własności materiału absorbenta.
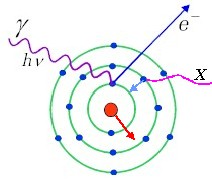 Rys.1.3.1 | Zjawisko fotoelektryczne, czyli pochłonięcie fotonu przez atom i emisja elektronu z powłoki leżącej w pobliżu jądra | |
|
| | |
| W wyniku zajścia tego procesu foton znika, atom zostaje zjonizowany, a wyemitowany elektron ma energię | ||
 | ||
| gdzie W jest tzw. pracą wyjścia odpowiadającą energii wiązania elektronu na orbicie atomowej. | ||
Zjawisko fotoelektryczne zachodzić może wyłącznie dla elektronów związanych w atomach. Kinematyka wymaga, by cześć pędu fotonu przejęło trzecie ciało jakim jest jądro atomowe. Właśnie dlatego efekt fotoelektryczny zachodzi najczęściej dla elektronów znajdujących się na powłokach będących najbliżej jądra, chociaż z tym właśnie wiąże się też warunek wyrażony wzorem (2.3.4) określający minimalną energię fotonu przy której może zajść zjawisko fotoelektryczne. Najsilniej związane są elektrony na powłoce najbliższej jądru zwanej powłoką K. Dlatego energię fotonu umożliwiającą uwolnienie elektronu z tej powłoki nazywa się często krawędzią K.
Po uwolnieniu elektronu z powłoki w pobliżu jądra może nastąpić przeskok na tę powłokę elektronu z powłoki dalszej. Wyzwalana przy tym energia emitowana jest w postaci kwantu promieniowania elektromagnetycznego w zakresie rentgenowskim. Może też nastąpić przekazanie energii innemu elektronowi w atomie i jego emisja. Elektron taki nazywany jest elektronem Auger'a.
Przekrój czynny na zjawisko fotoelektryczne rośnie bardzo szybko ze wzrostem liczby atomowej materiału w którym efekt zachodzi oraz maleje ze wzrostem energii samego fotonu. Można to zapisać w postaci empirycznej zależności
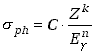 | (1.3.3) |
gdzie Z jest liczbą atomową materiału (absorbenta), a 
jest energią fotonu. Dla niskich energii (
) wartości wykładników potęg we wzorze (1.3.3) są: k=4.0, n=3.5; dla energii bardzo wysokich (
) k=4.6, n=1.0; C jest stałym, tj niezależnym od Z i 
,współczynnikiem proporcjonalności.
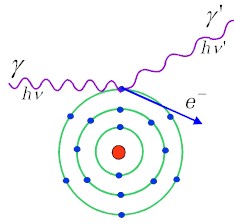 Rys.1.3.2 Efekt Comptona | Efekt Comptona, czyli rozproszenie fotonu na quasi-swobodnym elektronie. | |
|
| | |
| W rezultacie zajścia tego procesu foton zostaje rozproszony, a energia rozproszonego fotonu jest (oczywiście) mniejsza od energii fotonu pierwotnego. Jak już pokazaliśmy omawiając kinematyczne zależności w efekcie Comptona, energia rozproszonego fotonu jest też zależna od kąta rozproszenia.) | ||
 | ||
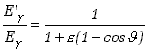| gdzie | ||
jest stosunkiem energii fotonu do energii spoczynkowej elektronu.Jak widać z postaci tego wzoru stosunek energii fotonu rozproszonego do energii fotonu pierwotnego ma najmniejszą wartość dla rozproszenia do tyłu, 
i zależny jest, poprzez wartość 
, od energii fotonu. Najsilniejsza zależność od kąta jest dla dużych energii.
Przekrój czynny na efekt Comptona określa wzór Kleina Nishiny, który ma złożoną formę. Dla dużych energii fotonów przekrój czynny na jeden elektron może być wyrażony prostą zależnością
 , |
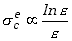z której widać, że przekrój czynny na efekt Comptona jest malejącą funkcją energii pierwotnego fotonu. W atomie, gdzie jest Z elektronów, przekrój czynny na jeden atom jest większy i określony jest zależnością: 
.
Zauważmy, że w przypadku efektu Comptona tylko część energii fotonu przekazana jest elektronowi; pozostałą unosi foton rozproszony. Przekrój czynny na efekt Comptona rozkładamy dlatego na dwa składniki: przekrój czynny na rozpraszanie 
oraz przekrój czynny na absorpcję, 
. Relację pomiędzy przekrojem czynnym na efekt Comptona, dany wzorem a jego składowymi przekrojami czynnymi można wyrazić w postaci
 |
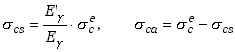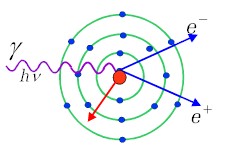 | Zjawisko tworzenia par elektron-pozyton polega na zamianie (konwersji) fotonu w parę: pozyton i elektron, tj.  . Proces ten możliwy jest jedynie, gdy energia fotonu przekracza pewną określoną wartość zwaną energią progową, co wynika z warunku spełnienia w tym procesie praw zachowania energii i pędu. Równoczesne spełnienie obu praw zachowania wymaga, by proces ten zachodził z udziałem "trzeciego ciała", jakim może być jądro atomowe lub elektron, nie może natomiast zachodzić w próżni. Przekaz energii i pędu zachodzi za pośrednictwem pola elektrostatycznego (kulombowskiego) jądra lub elektronu. Proces przebiega następująco: | |
| Rys.1.3.3 Tworzenie par |
| |
gdzie (A,Z) oznacza jądro o liczbie masowej A i atomowej Z.
Ze spełnienia praw zachowania wynika relacja określająca energię progową fotonu powyżej której może zachodzić zjawisko tworzenia par
 |
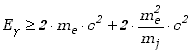gdzie 
jest energią fotonu, 
jest masą elektronu a 
masą jądra; 
- jest (oczywiście) prędkością światła. Ponieważ masa jądra jest tysiące razy większa niż masa elektronu, drugi człon we wzorze można zwykle zaniedbać wyrażając energię progową prostszym wzorem
 |
Oznacza to, że energia fotonu musi byś większa od energii odpowiadającej sumie mas pozytonu i elektronu, które to cząstki tworzone są w procesie konwersji.
Kiedy proces produkcji par zachodzi w polu elektrostatycznym elektronu, to energia progowa zgodnie ze wzorem, gdzie zamiast masy jądra wstawiamy masę elektronu, jest większa i wynosi
 |
Proces ten jest jednak znacznie mniej prawdopodobny niż konwersja w polu jądra.
Procesem odwrotnym do tworzenia par jest proces anihilacji pozytonu z elektronem, w którym para pozyton-elektron zamienia się na dwa fotony, tj. na dwa kwanty promieniowania elektromagnetycznego.
Przekrój czynny na wytworzenie pary przez foton o energii 
, w sąsiedztwie jądra o liczbie atomowej Z może być przedstawiony przybliżonym wzorem postaci
 |
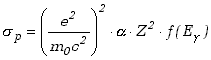gdzie 
, a 
rośnie logarytmiczne z energią fotonu, a przy energiach bardzo dużych przestaje zależeć od energii.